What3Words is a widely promoted system that is used for sharing a location using just three words. For example, ///wedge.drill.mess is located in Hyde Park.The globe is divided into 3m squares, each of which has a unique three word address to identify it.
They claim that mistakes – like changing a word into a plural, or adding an extra character – would result in a location so far away that you would detect the mistake. They have themselves stated “that people confuse plurals only about 5% of the time when hearing them read out loud”. This means the number of squares where this could be a problem is crucial. What3Words say the odds are “1 in 2.5 million” – but they seem to be under 1 in 100 in cities in the UK.
This might be OK if you are ordering takeaway, but if the application is directing emergency services to your location, these errors could cause serious problems.
If you just want the outcomes of this work, this shorter blog post might be a better read.
I’m going to describe the algorithm first and then go through the issues.
The Algorithm
What3Words can work entirely offline. A position is converted into words using an algorithm and a fixed word list of 40,000 words. This is described in their patent with enough level of detail that you can understand why it is fundamentally broken.
From a high level, the following steps are required:
- A lat/lon is converted into a integer coordinate XYxy.
- XYxy is converted into a single integer n representing position.
- n is shuffled into m to prevent words in two adjacent squares being the same.
- m is converted into i,j,k which index into the word list.
- i,j,k are converted into words.

Convert Lat/Lon to XYxy
The first step is to convert the decimal lat/lon into an integer XYxy location. This is just another type of grid reference with nothing complex going on.
The globe is divided up into large cells described by XY.
The Y direction starts at 0 at latitude -90° (the South Pole) and increases to 4,320 at latitude +90° (the North Pole). The X direction start at 0 at longitude -180° and increases to 8,640 at longitude +180°. This gives a total of 37,324,800 cells.
X increases as we move right, Y increases as we move up.
If we look in central London, we can see the scale of these cells. They are 4638m high and around 2885m across in London.
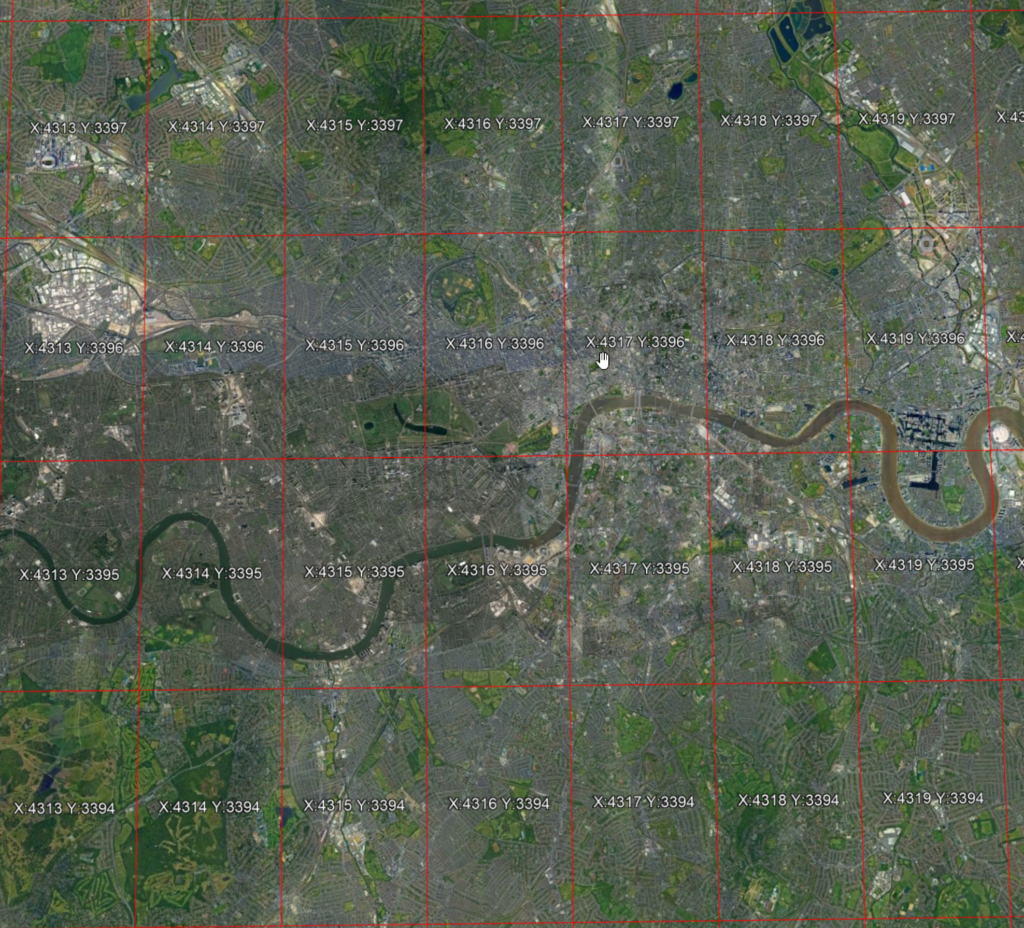
Within each of these large cells are the individual location squares, described by xy. There are always 1546 in the y direction. The number in the x direction varies from 1545 at the equator down to 1 at the poles. This is because of the curve of the earth.
In our central London cell of X=4316 Y=3396, x can range between 0 and 962, and y between 0 and 1546, giving 1,487,252 positions in the cell.
We now have an integer coordinate to represent anywhere on the earth.
Convert XYxy to n
The next step is to convert XYxy into n. n is a single large number that describes each point on the earth.
First, the offset into the large XY cell is found, using a simple formula:
1546 * x + y
This means that we are just counting upwards in columns as we go across. The bottom left corner of a cell is shown below. If you move up in the y direction, add one. If you move across in the x direction, add 1546. For the green square below, x=3 y=3 results in an offset of 4641.

Of course, this offset is not a unique number on the globe. To make it unique, the starting point – q – is defined for each XY cell.
In our central London square of X=4316 Y=3396, q = 733306450. That means the bottom left corner, n = 733306450. We add the offset on as we move through the cell. The n value of the green square is therefore 733311091 (733306450 + 4641).
The overall formula is:
n = q + 1546 * x + y
Where does q come from? Well, it comes from a lookup table.
Why is this done? q is used to bias lower values of n into cities. Lower values of n are important in the next steps.
We now have a large integer n, describing each point on the earth.
Convert n to m
The n value increases entirely predictably as we move through a cell. This could lead to the words for each position only changing by one word as we move about.
To handle this, a shuffling step is added to convert n to m. This step is also used to reduce the range of words used in cities to shorter and less complex words so that the system is easier to use.
The n values are split into bands. The bands go 0 to 2500^3 -1, 2500^3 to 5000^3 -1 all the way up to 37500-40000^3 -1. 16 bands in total. I’m only going to be looking at the first band from now onwards.
The shuffing within each band is carried out using the following formula:
m = StartOfBand + (BigNumber * PositionInBand) mod SizeOfBand
The BigNumber changes for each band. For band 0, from 0 to 2500^3 – 1, we get the following formula:
m = (9401181443 * n) mod 2500^3
The modulus means that the range of m will never be greater than 2500^3. In combination with the next step, this means that only the first 2,500 words in the dictionary are going to be used in band 0 cells.
For our example cell above with an n of 733311091, we have an m of 9813662131.
We now have a shuffled value m, another large integer.
Convert m to ijk
The single integer m now needs to be converted into three indices i,j,k into the 40,000 long word list.
The maths here is not particularly important. What is important is that this step does nothing to mask or shuffle how the value in m has changed.
For incrementing values of m, the pattern can clearly be seen in the output:
872848985 (39, 949, 955)
872848986 (39, 950, 955)
872848987 (39, 951, 955)
872848988 (39, 952, 955)
872848989 (39, 953, 955)
872848990 (39, 954, 955)
872848991 (40, 0, 955)
872848992 (40, 1, 955)
872848993 (40, 2, 955)
872848994 (40, 3, 955)
872848995 (40, 4, 955)
You can observe that below 2500^3, the three indices will always be 2499 or below. This means that the band 0 of n/m below 2500^3 will only ever result in the first 2,500 words out of the 40,000 being used.
2500^3 -5 (2498, 2494, 2499)
2500^3 -4 (2498, 2495, 2499)
2500^3 -3 (2498, 2496, 2499)
2500^3 -2 (2498, 2497, 2499)
2500^3 -1 (2498, 2498, 2499)
2500^3 0 (2499, 0, 2499)
2500^3 +1 (2500, 0, 1)
2500^3 +2 (2500, 0, 2)
2500^3 +3 (2500, 0, 3)
2500^3 +4 (2500, 0, 4)
2500^3 +5 (2500, 0, 5)
ijk (numbers) to Words
We have our i, j, k. These are three indices into a 40,000 long list of words.
If the word list was:
0 most
1 much
2 took
3 give
4 both
5 fact
6 help
7 ever
8 home
9 long
An i, j, k of 8, 4, 2 would give words of home.both.took with this example.
The word list is sorted so that shorter and less complex words are at the beginning, and longer and more complex ones at the end. The algorithm favours the start of the list for highly populous areas, thereby keeping the words short and simple.
For our example cell with an m of 9813662131, the i,j,k are 1940, 910, 2140 resulting in offers.trail.medium, right down in the bottom right of our large cell.
What does this all mean?
The design of the algorithm has resulted in some significant issues.
m periodicity
The conversion from n to m has some interesting characteristics.
m = (9401181443 * n) mod 2500^3
If we graph m for increasing n, you will spot a pattern.

Every 5th sample, the same pattern is seen. They might look identical in this graph, but each repeat is gradually increasing.
We can overlay these sequences from various values of n and see that the difference between the sequences varies. Sometimes they are close, sometimes they are far apart. This graph below shows m for n=0-4, n=133-137 and n=1023-1028.

After a certain number of sequences, the highest peak hits the limit of 2500^3 and has to wrap back down to 0 due to the modulus. You can see this happen in the graph below. The blue trace shows a continuous sample, increasing by a fixed amount each cycle. The orange one shows where it wraps, with a sharp jump downwards. This happens periodically, causing the position of the sequence to shift.

There are certain offsets in n that produce very closely matched sequences. It’s like two sine waves of slightly different frequencies coming in and out of phase to produce beat frequencies.
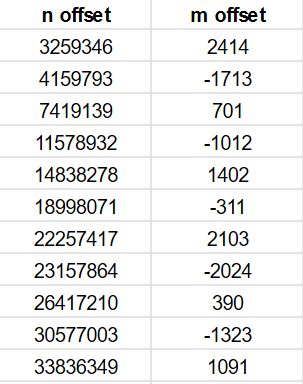
Just to illustrate this, we can plot values from the bottom corner of our large cell (X=4316 Y=3396, q = 733306450, n = 733306450) with an offset of 14838278 for n. The difference in m is small (1402) and constant in this range – the two lines overlay each other due to the large swings in value.

Small m offset results in two common words
When the offset between two n positions is from the list above, the difference between m for the two becomes constant and small.
There are over 500 of these n offsets resulting in an m offset of less than 2500. They can be generated automatically using a simple script.
The table below shows the n offset of 7,419,139 resulting in a m offset of 701.
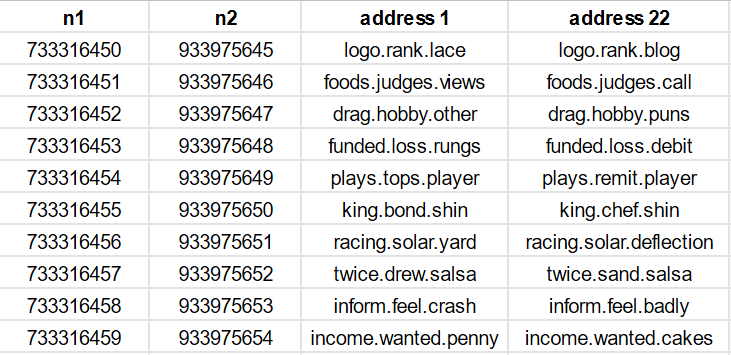
You can see how many of the address 1 and address 2 have one or two words in common.

So for every given cell, there are many other cells at fixed offsets where it is far more likely that two of the words are common. We can test his, choosing the ///daring.lion.race that What3Words use as the home address and testing lots of these offsets. You can see one or two words common in all the rows.

Notice how daring.hint is also very common.
For a given square, n, across all of these specific offsets, there appears to be around a 33% chance that two of the words match. I suspect it’s not 100% simply because I haven’t spotted a bigger pattern.
For a given offset, across a range of n, the probability massively varies. Offset 7,419,139 has around a 60% chance of two words matching. Offset 200,659,195 has a 99% chance of matching two words. The impact of this can be seen below – nearly all squares this far apart have two words in common.
Impact of limiting word list in cities
When talking about daring.lion.race, there are 39,999 other choices for the last word. We expect to find about 40,000 cells across the globe with the first two words common. It only becomes a problem when those cells are physically nearby.
If we were using the whole 40,000 word dictionary spread across the globe, then there is a 1 in 40000^2 chance that you pick a cell with the same two first words. That’s 1 in 1,600,000,000 – on average over 1000 cells away
But because we are in band 0 – the cities – and they only use the first 2500 words in the dictionary, we aren’t talking about 40,000 spread across the globe. We are talking about 2,500 words spread across a portion of the globe. We’re down to a 1 in 2500^2 chance – or 1 in 6,250,000 – in a much smaller area. This is just over 4 cells away – less than 12km.
And that is all that we are seeing – on average, we see two words match every 6,250,000 squares. By the time we have moved 500 cells away, we have seen 119 instances where the first two words are daring.lion. Around one in every 4 cells. This is a direct effect of limiting the word list to 2500 words in built-up areas.
So, we’ve shown that the first two words are going to match in nearby cells. But for that remaining different word, it’s unlikely that rush and stick would be confused, so why are we seeing plural pairs like take/takes?
Remember that the words are just the last step. They correspond to an ijk, three indices into the word list. Let’s look at ijk instead of the words. I am filtering the table for n offset 7,419,139 to only show addresses with two words in common, and I am showing the difference in the remaining word.
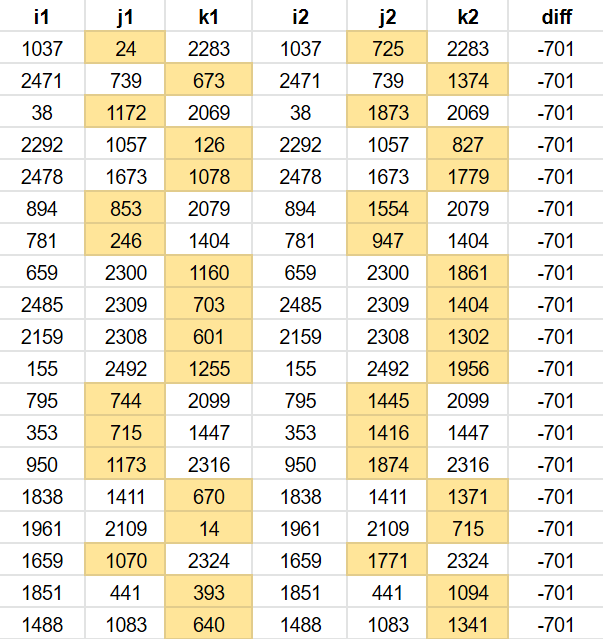
You might notice a pattern. The difference in the remaing word is always -701. This is because the conversion of m to ijk does little to mask changes in m. As the m offset is always -701, often one of i,j or k will also differ by 701.
Why is a difference of -701 in a word index a problem? Most of the time, this is just going to result in linked words pairs like stick/rush, neck/feels and so on.
But it’s also the difference between takes/take – position 726 and 25 in the wordlist.
Several of the m offsets that appear line up with other plural pairs:
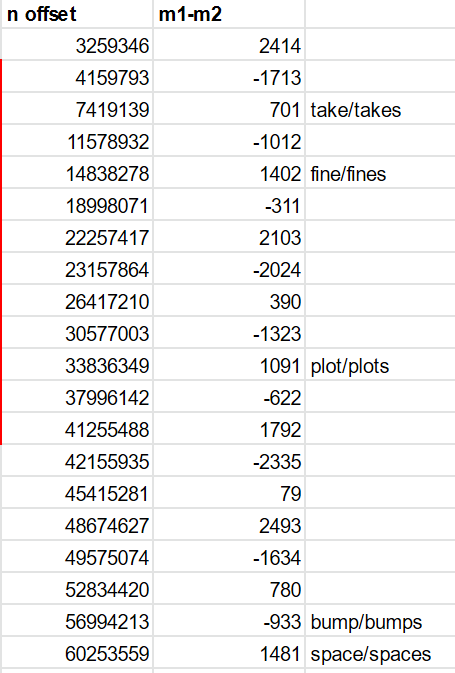
It is pure coincidence that two words, 701 apart in the wordlist, are a plural pair.
If we take a positive n offset, we see a word pair in one direction – take/takes. If we take a negative n offset, we see the word pair in the oppositve direction – takes/take..
How often do we see takes appear as the last word? Well, it turns out it’s only about as often we would expect for picking from a list of 2500 words – 1 in 2500 times.
Probability for nearby confusing pairs
If we pick one of the n offsets that cause problems – 7,419,139 causing take/takes – we can look at the chance that there are confusing pairs over a range of n. Let’s do that for n over our entire example cell.
For all squares in that cell, there are 876,541 squares offset by 7,419,139 that have two common words. That is 59% of the squares in the cell. 59% of the squares have the potential for the different word to be confused and that confusion to be within 7,419,139 distance in n away.
For those squares with two common words, 822 of them have the last word of takes. That means out of the entire cell, there is a 1 in 1800 chance that you pick a cell where the last word is takes and it could be changed to take to result in another location.
We need to check for negative n offset. There are 780 squares with the last word of take. This takes the chance of hitting one of the squares to around 1 in 930.
This wouldn’t be a problem if these linked squares were distant. But they aren’t. An n offset of 7,419,139 is only around 5 cells away.
This is easily demonstrated by testing for the pair take/takes on our cell and showing them on a map.
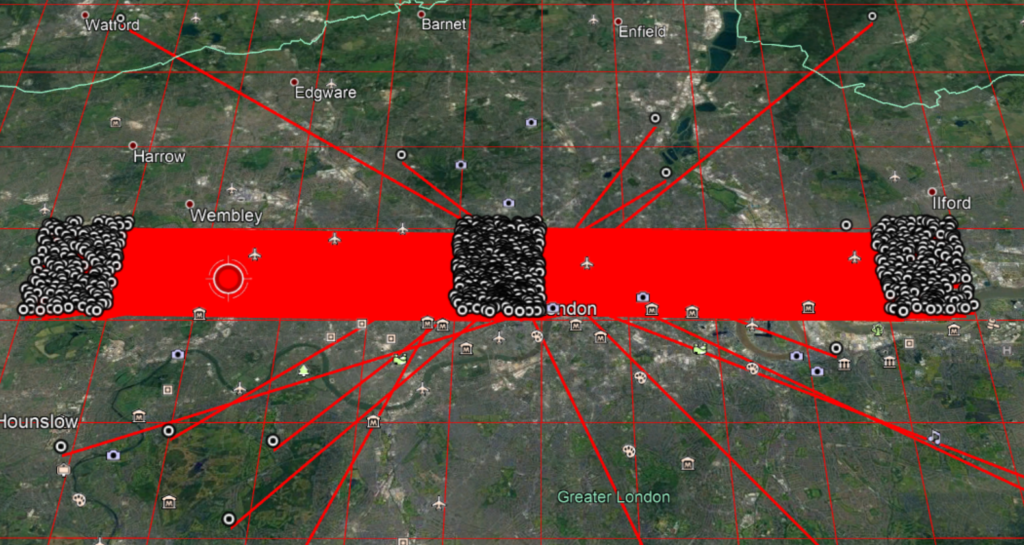
The cell to the right is the postive n offset, with the pair takes/take. The cell to the left is the negative n offset, with the pair take/takes.squares.
This behaviour is seen in every single cell in band 0. We can pick a cell, and there will be two other cells with take/takes relationships like this, around +/- 5 cells away.
Bigger n-offsets are not always distant
As we move down the list, the n offset gets larger and they start getting further and further away. bump/bumps – with an offset of 56,994,213 should be 38 cells away. So how are these a risk? First, let’s test for the pair bump/bumps on our example cell.

One of those is just over a single cell away – much closer than 38! Why has this happened?
The algorithm is designed to use only the first part of the word list in the most populous areas to improve usability.
We can show this on a map. All of the red cells are band 0 and yellow cells in band 2 (yes, there are no band 1 areas here).

All of those red cells are using a significantly limited dictionary of 2500 words instead of 40,000.
The band in which these cells fall is defined by setting the q value. We can find the q for cells using the API and show them on the map.

They are increasing left to right, and top to bottom. A more helpful representation is showing how many cells away from the start (q=0) they are. You can see London is right down at the start of the list, between 400 and 600 cells into the q values. These numbers might not be quite correct as I have just divided by an average cell size and rounded down.

Our example cell is 479 cells into q. bump/bumps should be around 38 cells away. 479 + 38 = 517. 479 -38 = 441. 517 and 441 are shown in red in the image blow.

It’s pretty clear to see these are the areas with a high density of issues on the plural pair bump/bumps.
This situation becomes even worse with some cells. Take a look at the centre of Birmingham here – the cell immediately below the one we are testing has a huge number of pairs.
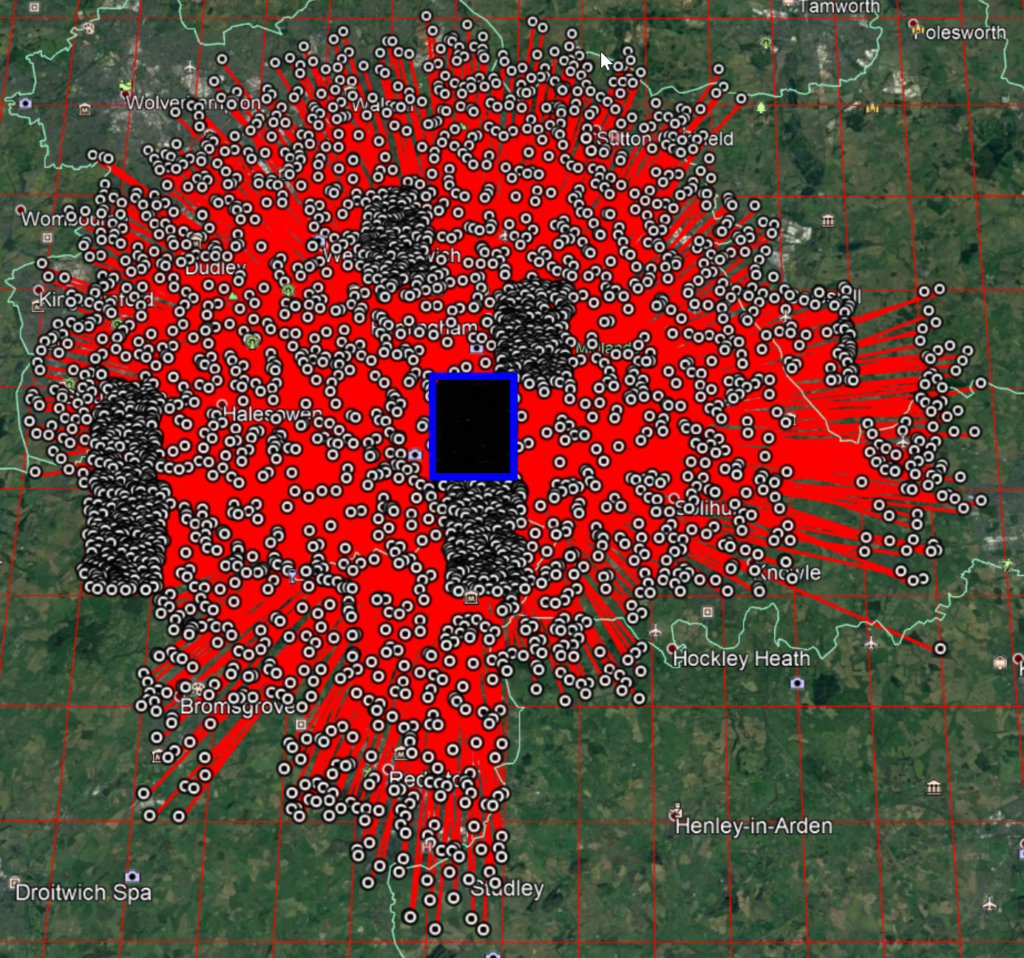
All of these have the word pair fine/fines – an m difference of 1402, which is an n offset of 14,838,278. This is around 10 cells of n away.

We just need to look at the q values though.
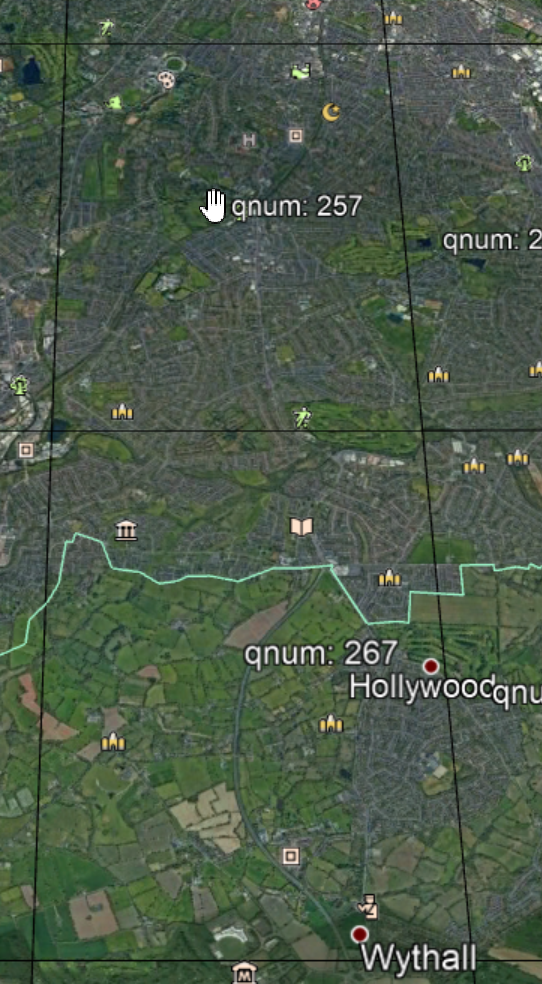
267 and 257 – 10 cells apart. When two cells end up adjacent and exhibit this issue, you get a large number of troublesome plural pairs – 535 pairs with only a single “s” different between two squares, all with a maximum distance of 9.3km between them.
The number of plurals
In the first 2,500 words, there are 354 words that can have an “s” added to them and that word is also in the list. That means 708 out of the 2,500 can be confused by adding or removing an “s”. This is a significant proportion.
When you look at this cumulatively, it results in about 63% of cells containing one or more of these words that can be confused. The distance that this confusion results in is variable, but with the above issues, it can often result in them being nearby.

The examples prior to now have looked at single cells with a given n offset. When you look at the bigger picture, the weaknesses in the algorithm become very apparent. The below map shows all of the plural pair confusions for our example cell that are inside London. There are 62,988 in the single cell.

There are odds of 1 in 24 that you hit one of these squares.

Conclusion
There are multiple issues with the What3Words algorithm.
For many squares in cities in the UK, there are a series of other squares which will only vary by one of the three words i.e. two of the words are common e.g. ///bank.fine.fishery and ///bank.fine.even. These relationship between these squares is predictable.
The distance between these squares that only vary by a word is often below 50km, but can be under 1km.
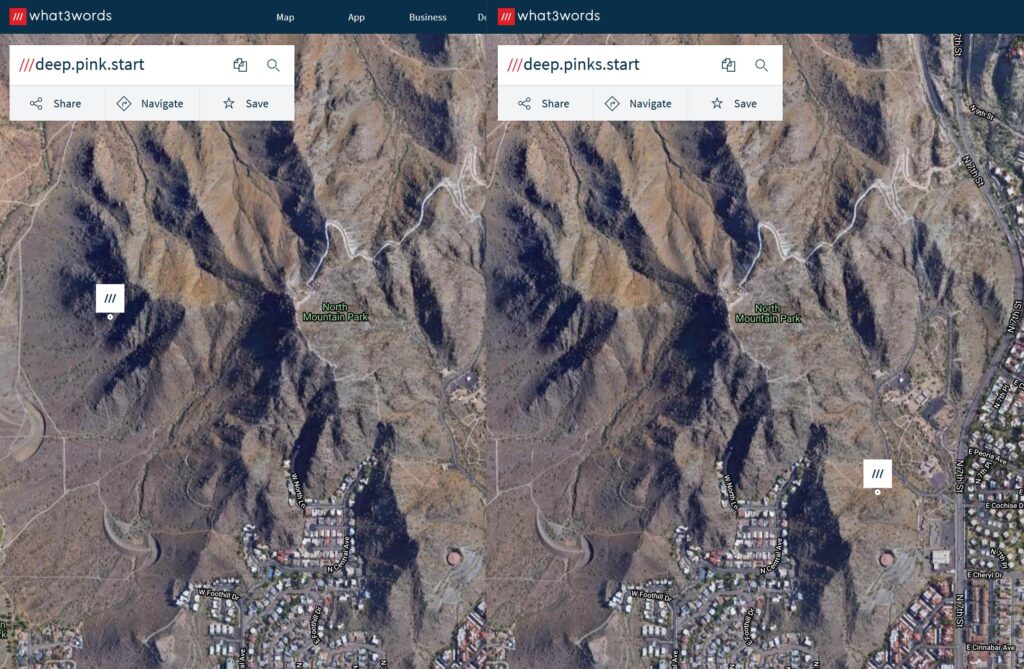
For some of these squares, the only variation in that remaining different word with be a single letter “s” e.g. ///bank.fine.fishery and ///bank.fines.fishery.
Certain word pairs – such as take/takes, fine/fines, plot/plots, bump/bumps and space/spaces – are more likely to result in close pairs.
This same issue can impact other errors such as spelling mistakes and homophones.
The word list is limited to 2,500 words in cities in the UK, greatly increasing the probability of these errors happening.
A side effect of defining these densely populated areas results in some of these pairs of squares being even closer than they would be normally.
Combining these issues means that there are many squares under 10km apart that can be confused by changing a word to and from a plural.